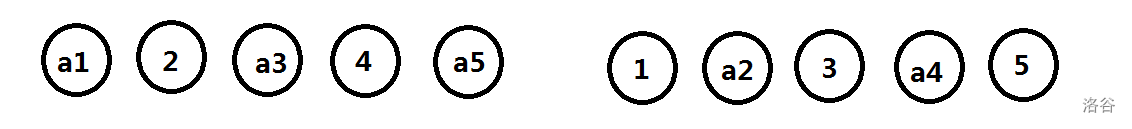# 二项式反演

# 公式

$$f_n = \sum_{i = 0}^n \dbinom {n}{i}g_i \Leftrightarrow g_n = \sum_{i = 0}^n (-1)^{n - i} \dbinom ni f_i$$

证明就不细说了。那么二项式反演的式子有什么用呢？

恰好和至多的转换：

设 $f_k$ 为恰好 $k$ 个的方案数，$g_k$ 为至多 $k$ 个的方案数（恰好 $k$ 个和至多 $k$ 个均为某种条件）。

假设可以快速计算出 $g_k$，我们要通过 $g_k$ 计算 $f_k$。

可以知道，$g_k = \sum\limits_{i = 1}^k \dbinom ki f_i$

（枚举恰好 $i$ 个满足条件，有 $k$ 选 $i$ 种方案，加起来）

根据二项式反演可以得出：

$$f_k = \sum_{i = 1}^k (-1)^{k - i} \dbinom ki g_i$$

恰好和至少的转换：

同理，设 $f_k$ 为恰好 $k$ 个的方案数，$g_k$ 为至少 $k$ 个的方案数。

有：

$$g_k = \sum_{i = k}^n \dbinom ki f_i$$

根据二项式反演：

$$f_k = \sum_{i = k}^n (-1)^{i - k} \dbinom ki g_i$$

# 例题

# P4859 已经没有什么好害怕的了

首先对 $a, b$ 从小到大排序。

设 $dp_{i, j}$ 表示前 $i$ 个 $a$ 中，至少有 $j$ 对 $a > b$，考虑如何转移。

分两种情况:

• $a_i$ 对 $j$ 没有贡献，那么加上 dp_

• $a_i$ 对 $j$ 有贡献，那么加上 $dp_{i - 1, j - 1} \times (p_i - (j - 1))$。$p_i$ 为最小的 $a_i > b$ 的 $b$ 的位置，由于 $b$ 是有序的，所以 $p_i$ 也是单调不降的。

写到一起：

$$dp_{i, j} = dp_{i - 1, j} + dp_{i - 1, j - 1} \times (p_i - (j - 1))$$

计算出 $dp$ 数组之后。设 $g_i$ 表示至少有 $k$ 对 $a > b$ 的方案数，即等于 $dp_{n, k} \times (n - k)!$。

乘上 $(n - k)!$ 是因为其他的可以随便排，只要保证至少有 $k$ 对 $a > b$ 即可。

再设 $f_k$ 表示恰好 $k$ 对 $a > b$ 的方案数，那么有 $g_k = \sum\limits_{i = k}^n \dbinom ik f_i$

根据二项式定理：

$$f_k = \sum_{i = k}^n (-1)^{k - i} \dbinom ik g_i$$

然后就可以计算出 $f_k$ 了。

需要注意的一个点，由于题目中要求的是 $a > b$ 的对数减去 $a < b$ 的对数为 $k$，所以 $a > b$ 的对数为 $\frac {n + k}2$。

# 斯特林数

# 第一类斯特林数

${n \brack k}$ 表示将 $n$ 个不同的数划分为 $k$ 个圆排列的方案数。

递推式：

$${n \brack k} = {n - 1\brack k - 1} + (n - 1) {n - 1 \brack k}$$

第 $n$ 个数单独一个圆排列，或者与前面的原排列合并到一起，放到任意一个数后面都行，所以乘上 $(n - 1)$。初值 ${0 \brack 0} = 0$。

# 第二类斯特林数

${n \brace m}$ 表示把 $n$ 个不同的数划分为 $k$ 个不计顺序的非空子集的方案数。

递推式：

$${n \brace k} = {n - 1 \brace k - 1} + k \times {n - 1 \brace k}$$

第 $n$ 个数单独在一个集合，或者 $n$ 合并到之前的集合中，有 $k$ 个集合。初值 ${0 \brace 0} = 1$

第二类斯特林数较为常用，且有如下公式：

$$m^n = \sum_{k = 0}^{min(n, m)} {n \brace k}\dbinom mk k!$$

证明：

考虑组合意义：

• 等式左边为 $n$ 个不同的球放到 $m$ 个不同的盒子的方案数。

• 右边：枚举非空盒子个数 $k$，先从 $m$ 个盒子中选 $k$ 个盒子，把 $n$ 个不同的球球划分到 $k$ 个盒子中，还要记盒子的顺序，所以再乘上 $k!$。

$${n \brace m} = \frac {1}{m!}\sum_{k = 0}^m (-1)^k \dbinom mk(m - k)^n$$

证明：

• 左边：把 $n$ 个球不同的球划分到 $m$ 个盒子中。

• 右边：容斥至少的空盒子个数，最后答案就是所有盒子非空的情况，盒子不考虑顺序，要除以 $m!$。

聪明伶俐的你一定发现了上面两个式子是符合二项式反演的！

简单推一下，先把第二个式子左右两边同乘 $m!$，并把等号右边的枚举空集合个数改成枚举非空集合，有：

$${n \brace m}m! = \sum_{k = 0}^m (-1)^{m - k} \dbinom {m}{m - k}k^n$$

设 $g_k = k^n, f_k = {n \brace k}k!$，容易看出：

$$g_m = \sum_{k = 0}^m \dbinom mk f_k \\ f_m = \sum_{k = 0}^m(-1)^{m - k} \dbinom mk g_k$$

正好就是二项式反演的式子。

# 例题

# P6620 [省选联考 2020 A 卷] 组合数问题

题目要求计算：

$$\left(\sum_{k=0}^{n}f(k)\times x^k\times \binom{n}{k}\right)\bmod p$$

但是一个多项式在里面显然很不好计算，考虑把多项式变成单项式，即：

$$\sum_{k = 0}^n \sum_{i = 0}^m a_i \times k^i \times x^k \times \dbinom nk$$

换一下求和顺序：

$$\sum_{i = 0}^m a_i \sum_{k = 0}^n k^i \times x^k \times \dbinom nk$$

这样一来，第二个求和号后面的部分就变成了单项式求求和。

考虑通过上面讲的公式把 $k^i$ 拆开，即：

$$\sum_{k = 0}^n (\sum_{j = 0}^i {i \brace j} \dbinom kj j!) \times x^k \times \dbinom nk$$

根据组合恒等式，$\dbinom nk \dbinom kj = \dbinom nj \dbinom {n - j}{k - j}$，有：

$$\sum_{k = 0}^n\sum_{j = 0}^i {i \brace j} \dbinom nj j! \times x^k \times \dbinom {n - j}{k - j}$$

再次交换求和顺序：

$$\sum_{j = 0}^i {i \brace j} \dbinom nj j! \sum_{k = 0}^n\dbinom {n - j}{k - j}x^k$$

考虑二项式定理的一般情况，$(x + 1)^n = \sum\limits_{i = 0}^n \dbinom nix^i$

令 $t = k - j$，有：

$$\sum_{j = 0}^i {i \brace j} n^{\underline j} \sum_{t = 0}^{n - j}\dbinom {n - j}{t}x^{t + j} \\ \sum_{j = 0}^i {i \brace j} n^{\underline j} \sum_{t = 0}^{n - j}\dbinom {n - j}{t}x^t \times x^j \\ \sum_{j = 0}^i {i \brace j} n^{\underline j} (1 + x)^{n - j}x^j$$

完整的式子：

$$\sum_{i = 0}^m a_i \sum_{j = 0}^i {i \brace j} n^{\underline j} (1 + x)^{n - j}x^j$$

不想预处理的话 $O(m^2 \log n)$ 也是可以过的。

# 斯特林数与阶乘幂

首先对于上升幂和下降幂有一种转换：

$$x^{\underline n} = (-1)^n(-x)^{\overline n} \\ x^{\overline n} = (-1)^n(-x)^{\underline n}$$

把上升下降幂展开模拟一下可以得到。

对于第一类斯特林数：

$$x^{\overline n} = \sum_{k = 0}^n {n \brack k}x^k$$

证明… 懒得写了（众所周知，OI 不需要证明）

对于第二类斯特林数：

$$n^m = \sum_{k = 0}^m {m \brace k} \dbinom nk k! = \sum_{k = 0}^m {m \brace k}n^{\underline k}$$

# 斯特林反演

与二项式反演类似：

$$g_n = \sum_{k = 0}^n {n \brace k}f_k \Leftrightarrow f_n = \sum_{k = 0}^n (-1)^{n - k} {n \brack k}g_k$$

证明不重要

# 例题

# [2018 雅礼集训 1-16] 方阵 (TopCoder-13444 CountTables)

题目描述

给出一个 $n \times m$ 大小的矩形，每个位置可以填上 $[1, c]$ 中的任意一个数，要求填好后任意两行互不等价且任意两列互不等价，两行或两列等价当且仅当对应位置完全相同，求方案数 。

$n, m \leq 5000$

题解

首先不考虑列的限制，如果只有每行互不等价的方案数为 $g_m = (c^m)^{\underline n}$。

设如果有 $m$ 列，且行列均互不等价的方案数为 $f_m$。

那么有:

$$g_m = \sum_{i = 0}^m {m \brace i} f_i$$

枚举等价的列的组数为 $i$，把 $m$ 列划分到 $i$ 组中，再乘上这 $n$ 行 $i$ 组列互不等价的方案数 $f_i$，即为 $g_m$。

然后就先计算出 $g_k$，再套斯特林反演计算 $f_m$ 即可。

# [BZOJ4671] 异或图

题目要求最终的图为一个连通图。

所以我们枚举有多少个联通块，设 $f_k$ 为恰好 $k$ 个联通块时的方案数，$g_k$ 为至少 $k$ 个联通快时的方案数，有：

$$g_k = \sum_{i = k}^n {i \brace k} f_i$$

把 $i$ 个联通块划分到 $k$ 个联通块中，再乘上 $f_i$。

根据斯特林反演得：

$$f_k = \sum_{i = k}^n (-1)^{i - k} {i \brack k}g_i$$

所以

$$f_1 = \sum_{i = 1}^n (-1)^{i - 1} {i \brack 1} g_i \\ f_1 = \sum_{i = 1}^n (-1)^{i - 1} (i - 1)!g_i$$

现在难点就在于如何计算 $g_i$ 了，考虑枚举子集划分。连接两个集合的边亦或值必须是 0，子集内的边不用管。

然后对于每一个划分，用线性基找出边集的极大线性无关组，记为 $tot$，方案数就是 $2^{m - tot}$。

# Catalan 数

# 定义

$C_0 = C_1 = 1$

递推式：

$$C_n = \sum_{i = 1}^n C_{i - 1}C_{n - i}$$

通项公式：

$$C_n = \dbinom {2n}n \frac 1{n + 1} = \dbinom {2n}n - \dbinom {2n}{n + 1}$$

生成函数（OGF）：

$$H(x) = \frac {1 - \sqrt{1 - 4x}}{2x}$$

证明：

$$\begin{aligned} H(x) =& \sum_{n \geq 0} H_nx^n \\ =& 1 + \sum_{n \geq 1}H_nx^n \\ =& 1 + \sum_{n \geq 1}\sum_{i = 0}^{n - 1} H_ix^iH_{n - i - 1}x^{n - i - 1}x \\ =& 1 + x\sum_{i \geq 0} H_ix^i\sum_{n \geq 0} H_nx^n \\ =& 1 + xH^2(x) \end{aligned}$$

解方程得：

$$H(x) = \frac {1 \pm \sqrt{1 - 4x}}{2x}$$

当取正号时，令 $x$ 趋近于 0，计算出 $H_0$ 为正无穷，而不是 1（不收敛），舍弃。所以应取负号。

# 组合意义

• 括号序列数（前缀 ( 个数不小于 ) 个数）。

• 进栈序列为 $1, 2, 3\cdots n$ 的出栈序列数。

• 将正 $n + 2$ 边形进行三角剖分方案数。

• $n$ 个节点的不同二叉树个数。

• 从 $(0, 0)$ 走到 $(n, n)$，且不能经过直线 $y = x + 1$ 的方案数。

  首先所有路径个数为 $\dbinom {2n}n$，减去不合法的，即经过 $y = x + 1$ 的路径。

  把第一次经过 $y = x + 1$ 的点及之后的点全都与 $y = x + 1$ 进行对称，最后的终点必定在 $(n - 1, n + 1)$ 上。

  路径数为 $\dbinom {2n}{n + 1}$，减去就行了。

# 杂题选讲

# P2523 [HAOI2011]Problem c

记一下后缀确定位置个数和 $s_i$，如果 $s_i > n - i + 1$ 那么无解。

考虑 $\text{dp}$，设 $f_{i, j}$ 表示剩余 $n - m$ 人中，编号 $\geq i$ 的人，已经确定了 $j$ 个人的方案数。

转移方程:

$$f_{i, j} = \sum_{k = 0}^j \dbinom jk f_{i + 1, j - k}$$

即枚举在第 $i$ 个位置确定 $k$ 个人，从 $j$ 里选 $k$ 个，乘上 $f_{i + 1, j - k}$。

答案为 $f_{1, n - m}$。

# P4456 [CQOI2018] 交错序列

考虑对贡献进行转化：

$$\begin{aligned} x^ay^b =& (n - y)^ay^b \\ =& \sum_{i = 0}^a \dbinom ai n^i(-y)^{a - i}y^b \\ =& \sum_{i = 0}^a (-1)^{a - i}\dbinom ai n^i y^{a + b - i} \end{aligned}$$

此时我们只需要计算 1 的个数即可，考虑如何维护 $y^x$。

设 $f_{i, j, 0/1}$ 表示考虑了前 $i$ 位，最后一位为 $0/1$，合法的序列 1 的个数的 $j$ 次方和。

转移方程：

• 结尾为 0：

  $$f_{i, j, 0} = f_{i - 1, j, 0} + f_{i - 1, j, 1}$$

  第 $i$ 位是 0，不影响 1 的个数，且前面一位填 0 或 1 均可。

• 结尾为 1：

  多了一个 1，贡献从 $y^j \rightarrow (y + 1)^j$，即 $\sum\limits_{k = 0}^j\dbinom jky^k$。

  所以有转移方程：

  $$f_{i, j, 1} = \sum\limits_{k = 0}^j\dbinom jk f_{i - 1, k, 0}$$

  因为最后一位为 1，前面一位只能填 0.

发现转移和 $i$ 无关，对 $i$ 进行矩阵快速幂。

$f$ 数组长成这样：

$$[f_{0,0}, f_{1,0}, f_{2,0}\cdots f_{a+b,0}, f_{0,1}, f_{1,1}\cdots f_{a + b, 1}]$$

转移矩阵分成 4 个部分：

• 左上角：单位矩阵

• 左下角：单位矩阵

• 右上角：二项式系数，不过要横过来

• 右下角：全是 0

（自己推一下应该不难验证是对的）

最后枚举一下计算答案即可。

# CF1188C Array Beauty

首先对 $a$ 从小到大排序，不影响答案。答案上界为 $\frac {a_n - a_1}{k - 1}$。

考虑枚举美丽值 $v$，然后计算美丽值为 $v$ 的子序列个数。

设 $f_{i, j}$ 表示美丽值大于等于 $v$ 的情况下，前 $i$ 个数选了 $j$ 个的方案数。

转移方程：

$$f_{i, j} = \sum_{a_i - a_k \geq v}f_{k, j - 1}$$

不难发现 $k$ 是单调不降的，维护一个指针即可。

时间复杂度 $O(nk\frac Vk)$，即 $O(nV)$。

需要注意的是，我们 $\text{dp}$ 出来的值是美丽值大于等于枚举的 $v$ 的方案数，所以有两种写法：

• 倒着枚举 $v$，每次贡献为 $v \times (now - lst)$。

• 正着枚举 $v$，每次贡献为 $now$。

（$now, lst$ 分别为美丽值大于等于 $v$ 的方案数和美丽值大于等于 $v + 1$ 的方案数）

# AT2370 [AGC013D] Piling Up

我们记录白球的个数为 $x$，那么黑球个数为 $n - x$。

操作可以分为 4 种情况：

• 先取白球，加入一白一黑，再取白球。

• 先取白球，加入一白一黑，再取黑球。

• 先取黑球，加入一白一黑，再取白球。

• 先取黑球，加入一白一黑，再取黑球。

4 种情况对白球个数的影响分别为 $-1, 0, 0, +1$。

设 $f_{i, j}$ 表示进行了 $i$ 次操作，当前有 $j$ 个白球的方案数。初值，$f_{0, i} = 1$.

转移方程:

• 若 $j \geq 1$:

  $$f_{i + 1, j - 1} += f_{i, j} \\ f_{i + 1, j} += f_{i, j}$$

• 若 $j < n$:

  $$f_{i + 1, j} += f_{i, j} \\ f_{i + 1, j + 1} += f_{i, j}$$

但是实际上这样是有问题的，初始时白球个数不同，相同的操作序列我们也会计算多次。

如何才能不重复计数呢？

考虑一个操作序列每次操作之后白球个数形成的折线。初始时白球个数不同只会导致这条折线上下平移。对于每条折线我们只算一次就行了。

不难发现，我们只计算碰到 $x$ 轴的折线个数即可。

所以还要开个 $\text{dp}$ 数组记录碰到 $x$ 轴的方案数。

设 $f_{i, j}$（$i, j$ 含义同上面）表示碰到 $x$ 轴的方案数，$g_{i, j}$ 表示没有碰到的方案数。

转移的时候判一下给谁转移就行。

# AT2062 [AGC005D] ~K Perm Counting

直接计算不是很好算，考虑容斥。

设 $f(m)$ 表示排列中至少有 $m$ 个 $|p_i - i| = k$ 的方案数。

$$Ans = \sum_{i = 0}^n(-1)^if_i$$

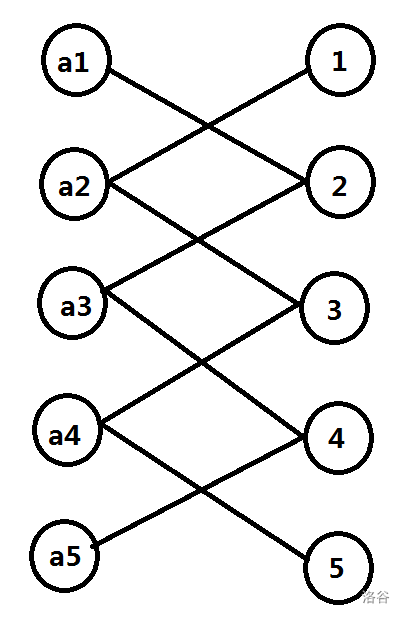
借用一下 @ez_lcw 的图：

这是 $n = 5, k = 1$ 时的图，左边为点，右边为权值。

连边则表示 $|p_i - i| = k$。此时我们要选出一些边，且任意两条边不能在同一个点上。

把这些点平铺：

此时要使 $|p_i - i| = k$，那么必须是相邻两个点连边。

设 $dp_{i, j, 0/1}$ 表示考虑了前 $i$ 个点，连了 $j$ 条边，第 $i - 1$ 个点和第 $i$ 个点之间是否连边。

转移方程：

$$dp_{i, j, 0} = dp_{i - 1, j, 0} + dp_{i - 1, j, 1} \\ dp_{i, j, 1} = dp_{i - 1, j - 1, 0}$$

需要注意一点，上图中 $a_5$ 和 1 之间不能连边，所以转移时也要特判一下。

我们已经有了 $dp$ 数组之后，$f_m = dp_{2n, m} \times (n - m)!$，然后计算答案即可。

# P4345 [SHOI2015] 超能粒子炮・改

答案为：

$$f(n, k) = \sum_{i = 0}^k \dbinom ni \bmod P$$

然后就是一波愉快的推式子：

$$\begin{aligned} f(n, k) =& \sum_{i = 0}^k \dbinom ni\bmod P \\ =& \sum_{i = 0}^k \dbinom {n / P}{i / P} \dbinom {n \% P}{i \% P} \\ \end{aligned}$$

根据 $i / P$ 可以把式子分成几段：

$$= \dbinom {n / P}0 \sum_{i = 0}^{P - 1}\dbinom {n \% P}{i} + \dbinom {n / P}1 \sum_{i = 0}^{P - 1}\dbinom {n \% P}{i} + \cdots +\dbinom {n / P}{k / P} \sum_{i = 0}^{k \% P}\dbinom {n \% P}{i}$$

除了最后一项前面的都可以合并起来：

$$\begin{aligned} f(n, k) =& \sum_{i = 0}^{P - 1}\dbinom {n \% P}i\sum_{j = 0}^{P/k - 1}\dbinom {n / P}j + \dbinom {n / P}{k / P} \sum_{i = 0}^{k \% P}\dbinom {n \% P}{i} \\ = &f(n \% P, P - 1) \times f(n / P, P / k - 1) + \dbinom {n / P}{k / P}f(n \% P, k \% P) \end{aligned}$$

预处理到 $f(P, P)$，组合数直接 $\text{Lucas}$，递归求解即可。

时间复杂度 $O(P^2 + T\log^2_{p}n)$。

# 群论

# 置换

定义

有限集合到自身的双射（即一一对应）称为置换。集合 $S = \left\{a_1, a_2, \cdots ,a_n \right\}$ 的置换可以表示为：

$$f = \begin{pmatrix}a_1, a_2, \cdots , a_n\\ a_{p_1}, a_{p_2}, \cdots ,a_{p_n}\end{pmatrix}$$

$p_1, p_2, \cdots, p_n$ 为一个 $1 \sim n$ 的排列，显然置换个数为 $n!$。

置换的乘法

置换的乘法是置换的叠加，如对于置换 $f = \begin{pmatrix}a_1, a_2, \cdots , a_n\\ a_{p_1}, a_{p_2}, \cdots ,a_{p_n}\end{pmatrix}$ 和 $g = \begin{pmatrix}a_{p_1}, a_{p_2}, \cdots , a_{p_n}\\ a_{q_1}, a_{q_2}, \cdots ,a_{q_n}\end{pmatrix}$，置换的乘积 $f \circ g$ 为：

$$f \circ g = \begin{pmatrix}a_1, a_2, \cdots , a_n\\ a_{q_1}, a_{q_2}, \cdots ,a_{q_n}\end{pmatrix}$$

# 置换群

集合 $S$ 的所有置换构成一个群，这个群的任意子群称为置换群。

置换群中的元素是置换。

# 轨道 - 稳定化子定理

（这个定理是为了证明 $\text{Burnside's}$ 引理，所以不看也没关系 /kk）

设 $G$ 为置换群，$X$ 为一种操作所有方案的集合（看不懂的话下面有例子）。

对于 $\forall x \in X$，$G(x) = \left\{f(x) | f \in G \right\}$ 称为 $x$ 的轨道，$G_x = \left\{f|f(x) = x, f \in G\right\}$ 称为 $x$ 的稳定化子。

轨道 - 稳定化子定理： $|G(x)||G^x| = |G|$

（对于置换 $f$，满足 $f(x) = x$ 的元素称为该置换的不动点。）

# Burnside 引理

设 $G$ 是集合 $X$ 上的置换群，$c(f)$ 为置换 $f$ 的不动点个数，若 $G$ 把集合 $X$ 分为了 $L$ 个等价类，则有：

$$L = \frac 1{|G|}\sum_{f \in G}c(f)$$

证明:

若集合中一个元素 $x$ 的轨道大小为 $|G(x)|$，那么有 $|G(x)|$ 个元素的轨道都相同，每个元素的贡献为 $\frac 1{G(x)}$。

$$\begin{aligned} L =& \sum_{x \in X}\frac 1{|G(x)|} \\ =& \frac 1{|G|}\sum_{x \in X} |G_x| \\ =& \frac 1{|G|}\sum_{f \in G} c(f) \end{aligned}$$

例子：

一个 4 个点的环，染黑白两种颜色，循环同构，求本质不同方案数。

集合 $X$：不考虑重复的染色方案，共有 $2^{4}$ 种。

不动点：旋转之后四个点的颜色与旋转之前一样，这样的染色方案叫做不动点。

置换群：置换群大小为 4，有 $f_0, f_1, f_2, f_3$ 4 种置换，$f_i$ 表示旋转 $i$ 次。

$L$：即为本质不同染色方案数。

$$\begin{aligned} L =& \frac 1{|G|}\sum_{f \in G}c(f) \\ =& \frac 1{|G|}(c(f_0) + c(f_1) + c(f_2) + c(f_3)) \\ =& \frac 1{4}(16 + 2 + 4 + 2) \\ =& 6 \end{aligned}$$

# Pólya 定理

$\text{Pólya}$ 定理提供了在特殊情况下计算不动点个数的方法。

考虑一种置换会形成许多置换环。

设 $h(f)$ 为置换 $f$ 的置换环数量，若要用 $k$ 种颜色给集合 $X$ 染色，那么有 $c(f) = k^{h(f)}$。

证明：

因为要计算不动点个数，所以一个置换环上面的点颜色必须都一样，有 $k$ 种选择。又由于一共有 $h(f)$ 个置换环，所以方案数为 $k^{h(f)}$。

进一步得：

$$L = \frac 1{|G|}\sum_{f \in G}k^{h(f)}$$

# 例题

# P4980 【模板】Pólya 定理

$\text{Pólya}$ 定理板题。

考虑如何计算置换环个数。

枚举旋转 $k$ 个，即从 1 旋转到 $k + 1$，那么循环节长度为 $\frac {lcm(n, k)}k$，所以共有 $\frac {n}{lcm(n, k) / k} = \gcd(n, k)$ 个循环节。

$$Ans = \frac 1n\sum_{k = 1}^nn^{\gcd(n, k)}$$

然后就要用到莫反基本功了。

$$\begin{aligned} Ans =& \frac 1n\sum_{k = 1}^nn^{\gcd(n, k)} \\ =& \frac 1n\sum_{d | n}n^d\sum_{k = 1}^{\frac nd}[\gcd(k, \frac nd) = 1] \\ =& \frac 1n\sum_{d|n}n^d\varphi(\frac nd) \end{aligned}$$

暴力计算 $\varphi$ 也可以通过。

# [POJ 1286] Necklace of Beads

题目描述

$n$ 个珠子串成一个圆，用 3 种颜色去涂色。问一共有多少种不同的涂色方法。（旋转和对称同构）

题解

旋转同构和对称同构分开考虑。

• 旋转：跟上面那道题是一样的，甚至直接暴力计算 $\gcd$ 都能过。

• 对称：

  • $n$ 为奇数：只能过一个端点对称，有 $n$ 个置换，每种置换有 $\frac {n + 1}2$ 个不同的置换环。

  • $n$ 为偶数：可以过两个端点对称，也可以切两条边对称。

    • 过端点：有 $\frac n2$ 个置换，每种置换有 $\frac n2 + 1$ 个置换环。

    • 过边：有 $\frac n2$ 个置换，每种置换 $\frac n2$ 个置换环。

置换群 $G$ 的大小为 $2n$，所以把上面所有情况都加起来之后再除以 $2n$ 就是答案。